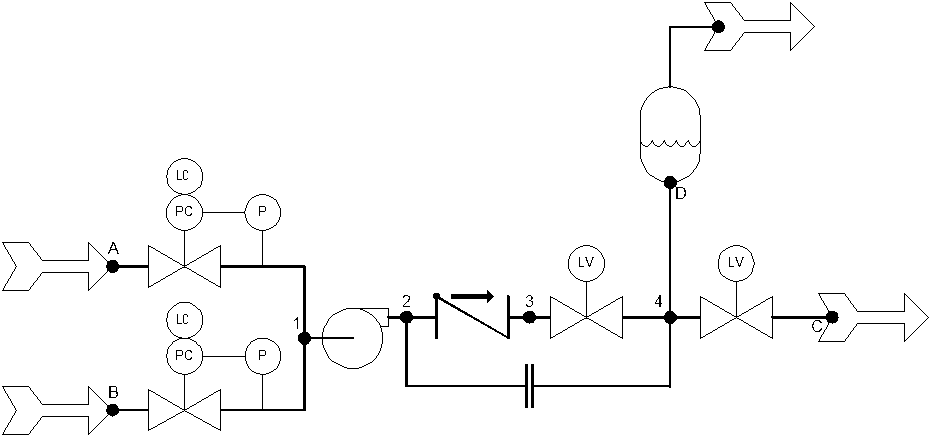
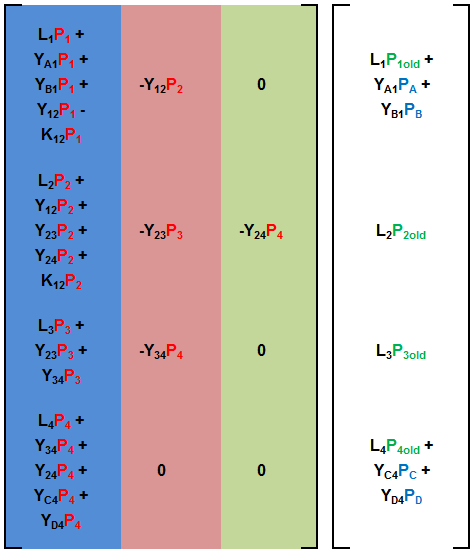
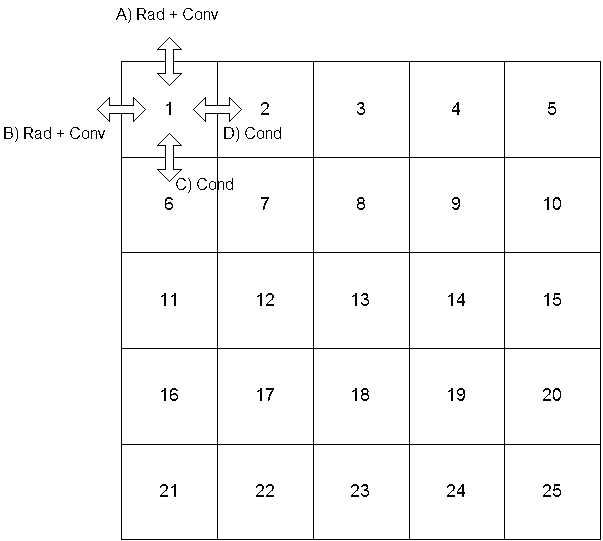
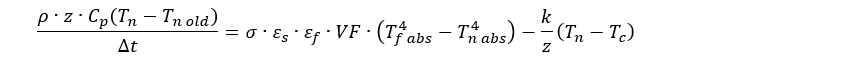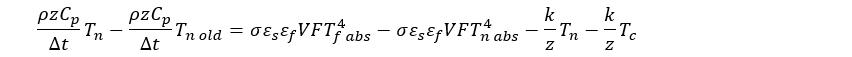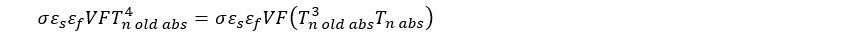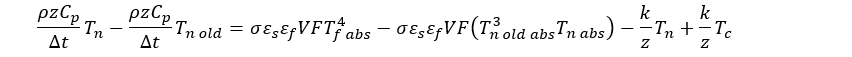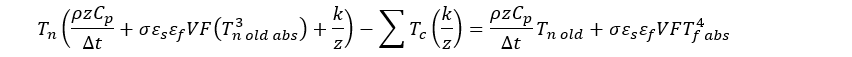C = raZMATX[ 1][1];
raZAUX[ 2] = raZMATX[ 1][ 2];
raZAUX[ 3] = raZMATX[ 1][ 3];
raZAUX[ 4] = raZMATX[ 1][ 4];
raZAUX[ 5] = raZMATX[ 1][ 5];
raZAUX[ 6] = raZMATX[ 1][ 6];
raZAUX[ 7] = raZMATX[ 1][ 7];
raZAUX[ 8] = raZMATX[ 1][ 8];
raZMATX[ 1][ 2] = raZMATX[ 1][ 2]/C;
raZMATX[ 1][ 3] = raZMATX[ 1][ 3]/C;
raZMATX[ 1][ 4] = raZMATX[ 1][ 4]/C;
raZMATX[ 1][ 5] = raZMATX[ 1][ 5]/C;
raZMATX[ 1][ 6] = raZMATX[ 1][ 6]/C;
raZMATX[ 1][ 7] = raZMATX[ 1][ 7]/C;
raZMATX[ 1][ 8] = raZMATX[ 1][ 8]/C;
raZSRCE[ 1] = raZSRCE[ 1]/C;
C = raZAUX[ 2];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 2][ 1] = raZMATX[ 2][ 1] - C*raZMATX[ 1][ 2];
raZMATX[ 2][ 2] = raZMATX[ 2][ 2] - C*raZMATX[ 1][ 3];
raZMATX[ 2][ 3] = raZMATX[ 2][ 3] - C*raZMATX[ 1][ 4];
raZMATX[ 2][ 4] = raZMATX[ 2][ 4] - C*raZMATX[ 1][ 5];
raZMATX[ 2][ 5] = raZMATX[ 2][ 5] - C*raZMATX[ 1][ 6];
raZMATX[ 2][ 6] = raZMATX[ 2][ 6] - C*raZMATX[ 1][ 7];
raZMATX[ 2][ 7] = raZMATX[ 2][ 7] - C*raZMATX[ 1][ 8];
raZSRCE[ 2] = raZSRCE[ 2] - C*raZSRCE[ 1];
}
C = raZAUX[ 3];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 3][ 1] = raZMATX[ 3][ 1] - C*raZMATX[ 1][ 3];
raZMATX[ 3][ 2] = raZMATX[ 3][ 2] - C*raZMATX[ 1][ 4];
raZMATX[ 3][ 3] = raZMATX[ 3][ 3] - C*raZMATX[ 1][ 5];
raZMATX[ 3][ 4] = raZMATX[ 3][ 4] - C*raZMATX[ 1][ 6];
raZMATX[ 3][ 5] = raZMATX[ 3][ 5] - C*raZMATX[ 1][ 7];
raZMATX[ 3][ 6] = raZMATX[ 3][ 6] - C*raZMATX[ 1][ 8];
raZSRCE[ 3] = raZSRCE[ 3] - C*raZSRCE[ 1];
}
C = raZAUX[ 4];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 4][ 1] = raZMATX[ 4][ 1] - C*raZMATX[ 1][ 4];
raZMATX[ 4][ 2] = raZMATX[ 4][ 2] - C*raZMATX[ 1][ 5];
raZMATX[ 4][ 3] = raZMATX[ 4][ 3] - C*raZMATX[ 1][ 6];
raZMATX[ 4][ 4] = raZMATX[ 4][ 4] - C*raZMATX[ 1][ 7];
raZMATX[ 4][ 5] = raZMATX[ 4][ 5] - C*raZMATX[ 1][ 8];
raZSRCE[ 4] = raZSRCE[ 4] - C*raZSRCE[ 1];
}
C = raZAUX[ 5];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 5][ 1] = raZMATX[ 5][ 1] - C*raZMATX[ 1][ 5];
raZMATX[ 5][ 2] = raZMATX[ 5][ 2] - C*raZMATX[ 1][ 6];
raZMATX[ 5][ 3] = raZMATX[ 5][ 3] - C*raZMATX[ 1][ 7];
raZMATX[ 5][ 4] = raZMATX[ 5][ 4] - C*raZMATX[ 1][ 8];
raZSRCE[ 5] = raZSRCE[ 5] - C*raZSRCE[ 1];
}
C = raZAUX[ 6];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 6][ 1] = raZMATX[ 6][ 1] - C*raZMATX[ 1][ 6];
raZMATX[ 6][ 2] = raZMATX[ 6][ 2] - C*raZMATX[ 1][ 7];
raZMATX[ 6][ 3] = raZMATX[ 6][ 3] - C*raZMATX[ 1][ 8];
raZSRCE[ 6] = raZSRCE[ 6] - C*raZSRCE[ 1];
}
C = raZAUX[ 7];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 7][ 1] = raZMATX[ 7][ 1] - C*raZMATX[ 1][ 7];
raZMATX[ 7][ 2] = raZMATX[ 7][ 2] - C*raZMATX[ 1][ 8];
raZSRCE[ 7] = raZSRCE[ 7] - C*raZSRCE[ 1];
}
C = raZAUX[ 8];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 8][ 1] = raZMATX[ 8][ 1] - C*raZMATX[ 1][ 8];
raZSRCE[ 8] = raZSRCE[ 8] - C*raZSRCE[ 1];
}
C = raZMATX[ 2][1];
raZAUX[ 2] = raZMATX[ 2][ 2];
raZAUX[ 3] = raZMATX[ 2][ 3];
raZAUX[ 4] = raZMATX[ 2][ 4];
raZAUX[ 5] = raZMATX[ 2][ 5];
raZAUX[ 6] = raZMATX[ 2][ 6];
raZAUX[ 7] = raZMATX[ 2][ 7];
raZAUX[ 8] = raZMATX[ 2][ 8];
raZMATX[ 2][ 2] = raZMATX[ 2][ 2]/C;
raZMATX[ 2][ 3] = raZMATX[ 2][ 3]/C;
raZMATX[ 2][ 4] = raZMATX[ 2][ 4]/C;
raZMATX[ 2][ 5] = raZMATX[ 2][ 5]/C;
raZMATX[ 2][ 6] = raZMATX[ 2][ 6]/C;
raZMATX[ 2][ 7] = raZMATX[ 2][ 7]/C;
raZMATX[ 2][ 8] = raZMATX[ 2][ 8]/C;
raZSRCE[ 2] = raZSRCE[ 2]/C;
C = raZAUX[ 2];
if ((C > 1.0E-10) || (C < -1.0E-10))
{
raZMATX[ 3][ 1] = raZMATX[ 3][ 1] - C*raZMATX[ 2][ 2];
raZMATX[ 3][ 2] = raZMATX[ 3][ 2] - C*raZMATX[ 2][ 3];
raZMATX[ 3][ 3] = raZMATX[ 3][ 3] - C*raZMATX[ 2][ 4];
raZMATX[ 3][ 4] = raZMATX[ 3][ 4] - C*raZMATX[ 2][ 5];
raZMATX[ 3][ 5] = raZMATX[ 3][ 5] - C*raZMATX[ 2][ 6];
raZMATX[ 3][ 6] = raZMATX[ 3][ 6] - C*raZMATX[ 2][ 7];
raZMATX[ 3][ 7] = raZMATX[ 3][ 7] - C*raZMATX[ 2][ 8];
raZSRCE[ 3] = raZSRCE[ 3] - C*raZSRCE[ 2];
}