Dividing a cross-section of a steel billet into nodes, we can start by looking at the energy balance for each node:

All this equation is saying is that the change in the quantity of energy in a given node per unit time is equal to the sum of the energy flows into and out of the node. The quantity to the left is the accumulation terms while the quantities on the right side of the equation are terms for radiative heat transfer from the environment to the surface of the steel, conductive heat transfer between nodes within the steel, convective heat transfer between the external atmosphere and the steel, and inductive heat transfer into the steel.
Let’s start by breaking the mass in the accumulator term down as follows:

We continue by eliminating the convection and induction terms because they are comparatively small or nonexistent, and then by dividing all the remaining terms by the unit area:
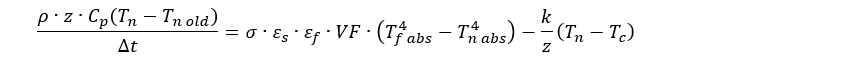
Next we can expand terms:
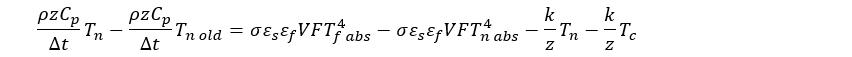
Steal a first order dependent variable from the fourth order term:
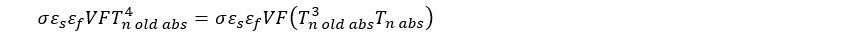
Substituting back into the previous equation yields:
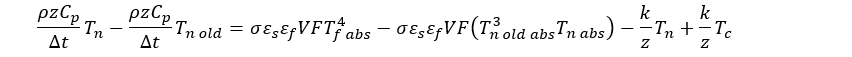
Gathering terms we get:
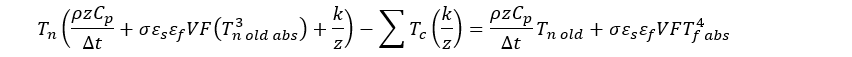
The coefficients for the Tn terms and the Tc terms on the left side of the equation fill the initialized coefficient matrix while the terms on the right side of the equation fill the initialized source matrix. There is one T term for each node. The radiation transfer terms drop out for any node that isn’t on the surface of the piece of steel being heated. The conduction terms drop out between any two nodes that aren’t internally connected.
This equation gets written for each node individually and then the system of equations gets solved. All of the Tn terms for the new time step end up in the source matrix at the end. Note that the temperatures are all represented in absolute degrees.
